| বাস্তৱ সংখ্যা সমাধান | |
| বিষয় (Subject) | গণিত (Mathematics) |
| কিতাপখনৰ নাম | সাধাৰণ গণিত |
| পাঠৰ নাম | বাস্তৱ সংখ্যা |
| শ্ৰেণী (Class) | দশম (X) |
| অধ্যায় (Chapter) | অধ্যায় 1 |
| অনুশীলনী | 1.1, 1.2, 1.3, 1.4 |
| পাঠ্যক্ৰম (Syllabus) | ছেবা (SEBA) |
বাস্তৱ সংখ্যা class 10
অধ্যায় – 1 বাস্তৱ সংখ্যা
অনুশীলনী 1.1
প্রঃ ইউক্লিডৰ কলনবিধি ব্যৱহাৰ কৰি গঃসাঃউঃ উলিওৱা-
i. 135 আৰু 225
প্ৰশ্নটোৰ পৰা 225 তকৈ 135 ডাঙৰ। সেয়েহে, ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি, আমি পাওঁ,
225 = 135 × 1 + 90
এতিয়া, বাকী 90 ≠ 0, এনেদৰে পুনৰ 90 ৰ বাবে বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি, আমি পাওঁ,
135 = 90 × 1 + 45
আকৌ, 45 ≠ 0, ওপৰোক্ত পদক্ষেপটো 45 ৰ বাবে পুনৰাবৃত্তি কৰি, আমি পাওঁ,
90 = 45 × 2 + 0
বাকী এতিয়া শূন্য, সেয়েহে আমাৰ পদ্ধতি ইয়াতে বন্ধ হয়। যিহেতু, অন্তিম পদক্ষেপত, ভাজক 45, সেয়েহে, গ:সা:গু: (225,135) = গ:সা:গু:(135, 90) = গ:সা:গু: (90, 45) = 45।
সেয়েহে, 225 আৰু 135 ৰ গ:সা:গু: হৈছে 45
ii. 196 আৰু 38220
এই প্ৰদত্ত প্ৰশ্নটোত, 38220>196, সেয়েহে ইউক্লিডৰ ইউক্লিডৰ বিভাজন প্ৰমেয়িকা প্ৰয়োগ কৰি আৰু 38220 ক ভাজ্য হিচাপে লৈ, আমি পাওঁ,
38220 = 196 × 195 + 0
আমি ইতিমধ্যে ইয়াত বাকী ০ পাইছো। সেয়েহে, গ:সা:গু: (196, 38220) = 196।
সেয়েহে, 196 আৰু 38220 ৰ গ:সা:গু: হৈছে 196।
iii. 867 and 255
এই প্ৰদত্ত প্ৰশ্নটোত, 867>255, সেয়েহে ইউক্লিডৰ ইউক্লিডৰ বিভাজন প্ৰমেয়িকা প্ৰয়োগ কৰি আৰু 867 ক ভাজ্য হিচাপে লৈ, আমি পাওঁ,
867 = 255 × 3 + 102
অৱশিষ্ট 102 ≠ 0, সেয়েহে 255 ক ভাজ্য হিচাপে লোৱা আৰু বিভাজন প্ৰমেয়িকা পদ্ধতি প্ৰয়োগ কৰা, আমি পাওঁ,
255 = 102 × 2 + 51
আকৌ, 51 ≠ 0। এতিয়া 102 হৈছে নতুন ভাজ্য, সেয়েহে আমি পোৱা একেই পদক্ষেপ পুনৰাবৃত্তি কৰা,
102 = 51 × 2 + 0
বাকী এতিয়া শূন্য, সেয়েহে আমাৰ প্ৰক্ৰিয়া ইয়াতে বন্ধ হয়। যিহেতু, অন্তিম পদক্ষেপত, ভাজক হৈছে 51, সেয়েহে, গ:সা:গু: (867,255) = গ:সা:গু: (255,102) = গ:সা:গু: (102,51) = 51।
সেয়েহে, 867 আৰু 255 ৰ গ:সা:গু: হৈছে 51।
প্ৰশ্ন 2 দেখুওৱা যে যিকোনাে যােগাত্মক অযুগ্ম অখণ্ড সংখ্যাই 6q +1, বা 6q + 3, বা 6q + 5 আৰ্হিৰ, য’ত q এটা কোনােবা অখণ্ড সংখ্যা।
সমাধান: ধৰা হ’ল,
a যিকোনো ধনাত্মক অযুগ্ম অখণ্ড সংখ্যা আৰু b = 6 হওঁক। তাৰ পিছত, বিভাজন প্ৰমেয়িকা দ্বাৰা, a= 6q + r, কিছুমান অখণ্ড সংখ্যা q ≥ 0 ৰ বাবে, আৰু r = 0, 1, 2, 3, 4, 5, কাৰণ 0≤r<6।
এতিয়া r-ৰ মান সলনি কৰি, আমি পাওঁ,
যদি, r = 0, তেন্তে a = 6q
একেদৰে, r= 1, 2, 3, 4 আৰু 5-ৰ বাবে, a’ৰ মান হৈছে ক্ৰমান্বয়ে 6q+1, 6কিউ+2, 6q+3, 6q+4 আৰু 6q+5।
যদি a = 6q, 6q+2, 6q+4, তেনেহ’লে এটা অযু সংখ্যা আৰু 2 ৰ দ্বাৰা বিভাজ্য। ধনাত্মক ইণ্টেগাৰ এটা যুগ্ম বা অযুগ্ম হ’ব পাৰে সেয়েহে, যিকোনো ধনাত্মক অযুগ্ম অখণ্ড সংখ্যা 6q+1, 6q+3 আৰু 6q+5 ৰ ৰূপৰ হয়, য’ত q হৈছে কিছু অখণ্ড সংখ্যা।
প্ৰশ্ন. 616 সদস্যৰ এটা সৈন্যবাহিনীৰ গােটে 32 জনীয়া এটা সেনাদলৰ পিছে পিছে কদম -খােজ কাঢ়ি যাবলগীয়া হ’ল। দুটো দলেই একে সমান সংখ্যক স্তম্ভত কদম-খােজ কাঢ়িবলগীয়া হ’ল।তেওঁলােকে খােজ কাঢ়িবলগীয়া স্তম্ভৰ উচ্চতম সংখ্যা কি হব?
সমাধানঃ 616 আৰু 32 ৰ গঃ সাঃ উঃ এই হৈছে নির্ণেয় স্তম্ভৰ উচ্চতম সংখ্যা।
ইয়াত, 616> 32
616 আৰু 32 ৰ ক্ষেত্ৰত বিভাজন প্রমেয়িকা প্রয়ােগ কৰি আমি পাওঁ,
616 = 32 x 19 + 8
যিহেতু 8≠ 0, গতিকে, 32 আৰু 8 ৰ ক্ষেত্ৰত বিভাজন প্রমেযিকা প্রয়ােগ কৰি আমি পাওঁ,
32 = ৪ x 4 + 0
এই পর্যায়ত ভাগশেষ শূন্য হৈছে। যিহেতু এই পর্যায়ত ভাজক 8, গতিকে, 616 আৰু 32 ৰ গঃ সাঃউঃ 8। গতিকে, নির্ণেয় স্তম্ভৰ উচ্চতম সংখ্যা 8
বাস্তৱ সংখ্যা class 10
Q. ইউক্লিডৰ ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি দেখুৱাব যে যিকোনো ধনাত্মক অখণ্ড সংখ্যা বৰ্গ টো 3m বা 3m + 1 প্ৰকাৰৰ হয়।
সমাধান:
ধৰা হল x যিকোনো ধনাত্মক অখণ্ড সংখ্যা আৰু y = 3।
তেনেহ’লে, ইউক্লিডৰ বিভাজন প্ৰমেয়িকা দ্বাৰা,
x = 3q + r কিছু অখণ্ড সংখ্যা বাবে q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.
সেয়েহে, x = 3q, 3q+1 আৰু 3q+2
এতিয়া দিয়া প্ৰশ্ন অনুসৰি,দুয়োফালে বৰ্গ কৰি, আমি পাওঁ,
x2 = (3q)2 = 9q2 = 3 × 3q2
ধৰা হল, 3q2 = m
সেয়েহে, x2= 3m …………..(1)
x2 = (3q + 1)2 = (3q)2+12+2×3q×1 = 9q2 + 1 +6q = 3(3q2+2q) +1
যোগ কৰি, 3q2+2q = m, to get,
x2= 3m + 1 ………………. (2)
x2= (3q + 2)2 = (3q)2+22+2×3q×2 = 9q2 + 4 + 12q = 3 (3q2 + 4q + 1)+1
আকৌ যোগ কৰি, 3q2+4q+1 = m, পাবলৈ,
x2= 3m + 1…………… (3)
সেয়েহে, সমীকৰণ 1, 2 আৰু 3-ৰ পৰা, আমি ক’ব পাৰোঁ যে, যিকোনো ধনাত্মক অখণ্ড সংখ্যা বৰ্গ টো 3m বা 3m + 1 প্ৰকাৰৰ প্ৰকাৰৰ হয়।
5. যিকোনো ধনাত্মক ইণ্টেগাৰৰ ঘন টো 9m, 9m + 1 or 9m + 8. প্ৰকাৰৰ হয়
সমাধান:
ধৰা হল x যিকোনো ধনাত্মক অখণ্ড সংখ্যা আৰু y = 3
তেনেহ’লে, ইউক্লিডৰ বিভাজন প্ৰমেয়িকা দ্বাৰা,
x = 3q+r, যত q≥0 আৰু r = 0, 1, 2, যেনেকৈ r ≥ 0 আৰু r < 3.
সেয়েহে, r-ৰ মান বহুৱাই, আমি পাওঁ,
x = 3q
বা
x = 3q + 1
বা
x = 3q + 2
এতিয়া, ওপৰোক্ত তিনিওটা অভিব্যক্তিৰ ঘন লৈ, আমি পাওঁ,
Case (i): যেতিয়া r = 0, তেতিয়া,
x3= (3q)3 = 27q3= 9(3q3)= 9m, যত m = 3q3
Case (ii): যেতিয়া r = 1, তেতিয়া,
x3 = (3q+1)3 = (3q)3 +13+3×3q×1(3q+1) = 27q3+1+27q2+9q
9 ক সাধাৰণ উৎপাদক হিচাপে লৈ, আমি পাওঁ,
x3 = 9(3q3+3q2+q)+1
m-ৰ মান বহুৱাই আমি পাওঁ,
m= (3q3+3q2+q) বহুৱাই আমি পাওঁ,
x3 = 9m+1
Case (iii): যেতিয়া r = 2, তেতিয়া,
x3 = (3q+2)3= (3q)3+23+3×3q×2(3q+2) = 27q3+54q2+36q+8
9 ক সাধাৰণ উৎপাদক হিচাপে লৈ
x3=9(3q3+6q2+4q)+8
m= (3q3+6q2+4q) বহুৱাই আমি পাওঁ,
x3 = 9m+8
সেয়েহে, ওপৰত বৰ্ণনা কৰা তিনিওটা ঘটনাৰ পৰা, এইটো প্ৰমাণিত হয় যে যিকোনো ধনাত্মক ইণ্টেগাৰৰ ঘন টো 9m, 9m + 1 or 9m + 8. প্ৰকাৰৰ হয়
বাস্তৱ সংখ্যা class 10 অনুশীলনী 1.2
১) সংখ্যাকে ইয়াৰ মৌলিক উৎপাদক বোৰৰ গুণফল হিচাপে প্ৰকাশ কৰা।
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
সমাধান সমূহ:
(i) 140
মৌলিক উৎপাদক বিশ্লেষণৰ দ্বাৰা আমি পাওঁ
140 = 2 × 2 × 5 × 7 × 1 = 22×5×7
(ii) 156
156 = 2 × 2 × 13 × 3 × 1 = 22× 13 × 3
(iii) 3825
3825 = 3 × 3 × 5 × 5 × 17 × 1 = 32×52×17
(iv) 5005
5005 = 5 × 7 × 11 × 13 × 1 = 5 × 7 × 11 × 13
(v) 7429
7429 = 17 × 19 × 23 × 1 = 17 × 19 × 23
দশম শ্ৰেণীৰ গণিত অধ্যায় ১
২) তলৰ অখণ্ড সংখ্যা কেইযোৰৰ লঃসাঃগুঃ উলিওৱা। সত্যাপন কৰা যে লঃসাঃগুঃ ×গঃসাঃগুঃ = সংখ্যা দুটাৰ পুৰণফল।
(i) 26 আৰু 91 (ii) 510 আৰু 92 (iii) 336 আৰু 54
সমাধানসমূহ:
(i) 26 আৰু 91
26 আৰু 91ৰ মৌলিক উৎপাদক বোৰৰ গুণফল হিচাপে প্ৰকাশ কৰি, আমি পাওঁ,
26 = 2 × 13 × 1
91 = 7 × 13 × 1
সেয়েহে, লঃসাঃগুঃ(26, 91) = 2 × 7 × 13 × 1 = 182
আৰু গঃসাঃগুঃ (26, 91) = 13
সত্যাপন
26 আৰু 91 সংখ্যা দুটাৰ পুৰণফল = 26 × 91 = 2366
লঃসাঃগুঃ ×গঃসাঃগুঃ = 182 × 13 = 2366
সেয়েহে,
লঃসাঃগুঃ ×গঃসাঃগুঃ = 26 আৰু 91 সংখ্যা দুটাৰ পুৰণফল
(ii) 510 আৰু 92
510 আৰু 92 ৰ মৌলিক উৎপাদক বোৰৰ গুণফল হিচাপে প্ৰকাশ কৰি, আমি পাওঁ,
510 = 2 × 3 × 17 × 5 × 1
92 = 2 × 2 × 23 × 1
সেয়েহে, লঃসাঃগুঃ(510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460
আৰু গঃসাঃগুঃ (510, 92) = 2
সত্যাপন
510 আৰু 92 সংখ্যা দুটাৰ পুৰণফল = 510 × 92 = 46920
লঃসাঃগুঃ ×গঃসাঃগুঃ = 23460 × 2 = 46920
সেয়েহে,
লঃসাঃগুঃ ×গঃসাঃগুঃ = 510 আৰু 92 সংখ্যা দুটাৰ পুৰণফল
(iii) 336 and 54
336 আৰু 54 ৰ মৌলিক উৎপাদক বোৰৰ গুণফল হিচাপে প্ৰকাশ কৰি, আমি পাওঁ,
336 = 2 × 2 × 2 × 2 × 7 × 3 × 1
54 = 2 × 3 × 3 × 3 × 1
সেয়েহে, লঃসাঃগুঃ(336, 54) = 3024
আৰু গঃসাঃগুঃ (336, 54) = 2×3 = 6
সত্যাপন
336 আৰু 54 সংখ্যা দুটাৰ পুৰণফল = 336 × 54 = 18,144
লঃসাঃগুঃ ×গঃসাঃগুঃ = 3024 × 6 = 18,144
সেয়েহে,
লঃসাঃগুঃ ×গঃসাঃগুঃ = 336 আৰু 54 সংখ্যা দুটাৰ পুৰণফল
বাস্তৱ সংখ্যা class 10
মৌলিক উৎপাদিকীকৰণ পদ্ধতিৰে তলৰ অখণ্ড সংখ্যাবোৰৰ লঃসাঃগুঃ আৰু গঃসাঃগুঃ উলিওৱা
(i) 12, 15 আৰু 21
(ii) 17, 23আৰু 29
(iii) 8, 9আৰু 25
সমাধানসমূহ:
(i) 12, 15 and 21
মৌলিক উৎপাদক বোৰৰ গুণফল হিচাপে প্ৰকাশ কৰি, আমি পাওঁ,
12=2×2×3
15=5×3
21=7×3
সেয়েহে,
গঃসাঃগুঃ (12,15,21) = 3
লঃসাঃগুঃ (12,15,21) = 2 × 2 × 3 × 5 × 7 = 420
(ii) 17, 23 and 29
মৌলিক উৎপাদক বোৰৰ গুণফল হিচাপে প্ৰকাশ কৰি, আমি পাওঁ,
12=2×2×3
15=5×3
21=7×3
সেয়েহে,
গঃসাঃগুঃ(17,23,29) = 1
লঃসাঃগুঃ(17,23,29) = 17 × 23 × 29 = 11339
(iii) 8, 9আৰু 25
মৌলিক উৎপাদক বোৰৰ গুণফল হিচাপে প্ৰকাশ কৰি, আমি পাওঁ,
8=2×2×2×1
9=3×3×1
25=5×5×1
সেয়েহে,
গঃসাঃগুঃ(8,9,25)=1
লঃসাঃগুঃ 2×2×2×3×3×5×5 = 1800
Q. দিয়া আছে (306, 657) =9 লঃসাঃগুঃ(306, 657) উলিওৱা
সমাধান: আমি সেইটো জানো,
লঃসাঃগুঃ ×গঃসাঃগুঃ = সংখ্যা দুটাৰ পুৰণফল
9 ×লঃসাঃগুঃ = 306 × 657
লঃসাঃগুঃ = (306×657)/9 = 22338
সেয়েহে, লঃসাঃগুঃ = (306×657)/9 = 22338
Q. যিকোনো স্বাভাৱিক সংখ্যা ৰ বাবে 6n অংক 0 ৰ সৈতে সমাপ্ত হ’ব পাৰে নে নাই পৰীক্ষা কৰক।
সমাধান: যদি 6n সংখ্যাটো শূন্য (0)ৰ সৈতে সমাপ্ত হয়, তেন্তে ইয়াক 5 ৰে বিভাজ্য কৰিব লাগে, কিয়নো আমি জানো যে 0 বা 5 হিচাপে একক স্থান থকা যিকোনো সংখ্যা 5 ৰ দ্বাৰা বিভাজ্য।
মৌলিক উৎপাদক 6n = (2×3)n
সেয়েহে, 6n-ৰ মৌলিক উৎপাদক কৰণত প্ৰাইম নম্বৰ 5 নাথাকে।
সেয়েহে, এয়া স্পষ্ট যে যিকোনো স্বাভাৱিক সংখ্যা n-ৰ বাবে, 6n 5 ৰ দ্বাৰা বিভাজ্য নহয় আৰু এনেদৰে ই প্ৰমাণ কৰে যে 6n যিকোনো স্বাভাৱিক সংখ্যাৰ বাবে অংক 0 ৰ সৈতে শেষ হ’ব নোৱাৰে।
6. কিয় 7 × 11 × 13 + 13 আৰু 7 × 6 × 5 × 4 × 3 × 2 × 2 × 1 + 5 যৌগিক সংখ্যা।
সমাধান: যৌগিক সংখ্যাৰ সংজ্ঞা অনুসৰি, আমি জানো, যদি এটা সংখ্যা যৌগিক হয়, তেন্তে ইয়াৰ অৰ্থ হৈছে ইয়াৰ 1 আৰু নিজৰ বাহিৰে আন কাৰক আছে। সেয়েহে, প্ৰদত্ত অভিব্যক্তিৰ বাবে;
7 × 11 × 13 + 13
13 ক সাধাৰণ উৎপাদক হিচাপে লওঁ, আমি পাওঁ,
=13(7×11×1+1) = 13(77+1) = 13×78 = 13×3×2×13
সেয়েহে, 7 × 11 × 13 + 13 হৈছে এক যৌগিক সংখ্যা।
এতিয়া আন নম্বৰটো লওঁ আহক,
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
5 ক সাধাৰণ উৎপাদক হিচাপে লওঁ, আমি পাওঁ,
=5(7×6×4×3×2×1+1) = 5(1008+1) = 5×1009
সেয়েহে, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 হৈছে এক যৌগিক সংখ্যা।
7. এটা ক্ৰীড়া ক্ষেত্ৰৰ চাৰিওফালে এটা বৃত্তাকাৰ পথ আছে। ছোনিয়াই খেলপথাৰৰ এটা ৰাউণ্ড চলাবলৈ 18 মিনিট সময় লয়, আনহাতে ৰবিয়ে ইয়াৰ বাবে 12 মিনিট সময় লয়। ধৰি লওঁক তেওঁলোক দুয়ো একে সময়তে আৰু একে সময়তে আৰম্ভ কৰে, আৰু একে দিশত যায়। কিমান মিনিটৰ পিছত তেওঁলোকে আৰম্ভণি বিন্দুত পুনৰ লগ পাব?
সমাধান: যিহেতু, ছোনিয়া আৰু ৰবি দুয়ো একে দিশত আগবাঢ়ে আৰু একে সময়তে, তেওঁলোকে আৰম্ভণি বিন্দুত পুনৰ লগ হ’ব সেই সময় উলিয়াবলৈ পদ্ধতিটো হৈছে 18 আৰু 12 ৰ লঃসাঃগুঃ
লঃসাঃগুঃ= (18,12) = 2×3×3×2×1=36
সেয়েহে, ছোনিয়া আৰু ৰবি 36 মিনিটৰ পিছত আৰম্ভণি বিন্দুত পুনৰ লগ হ’ব।
বাস্তৱ সংখ্যা class 10 অনুশীলনী 1.3
1. প্ৰমাণ কৰা যে √5 অপৰিমেয়।
সমাধান: আমি ধৰি লওঁ যে √5 হৈছেপৰিমেয় সংখ্যা।
অৰ্থাৎ √5 = x/y (য’ত, x আৰু y সহ-মৌলিক )
y√5= x
দুয়োফালে বৰ্গ কৰি, আমি পাওঁ,
(y√5)2 = x2
⇒5y2 = x2……………….. (1)
এনেদৰে, x2 5 ৰ দ্বাৰা বিভাজ্য হয়, সেয়েহে x ও 5-ৰ দ্বাৰা বিভাজ্য হয়।
আমি কওঁ, x = 5k, k-ৰ কিছু মানৰ বাবে আৰু সমীকৰণ (1) ত x মান প্ৰতিস্থাপন কৰক আমি পাওঁ,
5y2 = (5k)2
⇒y2 = 5k2
5 ৰ দ্বাৰা বিভাজ্য ইয়াৰ অৰ্থ হৈছে y ও 5 ৰ দ্বাৰা বিভাজ্য।
স্পষ্টকৈ, x আৰু y সহ-মৌলিক নহয়। সেয়েহে, √5 সম্পৰ্কে আমাৰ ধাৰণা যুক্তিসঙ্গত, অশুদ্ধ।
সেয়েহে, √5 হৈছে এক অপৰিমেয় সংখ্যা।
প্ৰমাণ কৰা যে 3 + 2√5 + অপৰিমেয়।
সমাধান: আমি ধৰি লওঁ 3 + 2√5 অপৰিমেয়।
তাৰ পিছত আমি সহ-মৌলিক x আৰু y (y ≠ 0) এনেদৰে বিচাৰি পাম যে 3 + 2√5 = x/y
পুনৰ সজ্জিত কৰি, আমি পাওঁ,
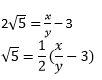
যিহেতু, x আৰু y হৈছে অখণ্ড সংখ্যা, এনেদৰে,
![]() এটা পৰিমেয় সংখ্যা।
এটা পৰিমেয় সংখ্যা।
সেয়েহে, √5 হৈছে এক পৰিমেয় সংখ্যা। কিন্তু ই এই সত্যৰ বিৰোধিতা কৰে যে √5 অপৰিমেয়। সেয়েহে, আমি এই সিদ্ধান্তত উপনীত হওঁ যে 3 + 2√5 অপৰিমেয়।
দশম শ্ৰেণীৰ গণিত অধ্যায় ১
3. প্ৰমাণ কৰা যে নিম্নলিখিতবোৰ অপৰিমেয়:
(i) 1/√2
(ii) 7√5
(iii) 6 + √2
সমাধানসমূহ:
(i) 1/√2
আমি ধৰি লওঁ যে 1/√2 পৰিমেয়।
তাৰ পিছত আমি সহ-মৌলিক x আৰু y (y ≠ 0) এনেদৰে বিচাৰি পাম যে1/√2 = x/y
পুনৰ সজ্জিত কৰি , আমি পাওঁ,
√2 = y/x
যিহেতু, x আৰু y হৈছে পূৰ্ণসংখ্যা, সেয়েহে, √2 হৈছে এক পৰিমেয় সংখ্যা, যি √2 অপৰিমেয় বুলি বিৰোধিতা কৰে।
সেয়েহে, আমি এই সিদ্ধান্তত উপনীত হ’ব পাৰোঁ যে 1/√2 অপৰিমেয়।
(ii) 7√5
আমি ধৰি লওঁ যে 7√5 পৰিমেয়।
তাৰ পিছত আমি সহ-মৌলিক x আৰু y (y ≠ 0) এনেদৰে বিচাৰি পাম যে 7√5 = x/y
পুনৰ সজ্জিত কৰি , আমি পাওঁ,
√5 = y/x
যিহেতু, x আৰু y হৈছে পূৰ্ণসংখ্যা, সেয়েহে, √5 হৈছে এক পৰিমেয় সংখ্যা, যি √5 অপৰিমেয় বুলি বিৰোধিতা কৰে।
সেয়েহে, আমি এই সিদ্ধান্তত উপনীত হ’ব পাৰোঁ যে 7√5 অপৰিমেয়।
(iii) 6 + √2
আমি ধৰি লওঁ যে 6 + √2 পৰিমেয়।
তাৰ পিছত আমি সহ-মৌলিক x আৰু y (y ≠ 0) এনেদৰে বিচাৰি পাম যে 6 + √2 = x/y
পুনৰ সজ্জিত কৰি , আমি পাওঁ,
√2 = (x/y) – 6
যিহেতু, x আৰু y হৈছে পূৰ্ণসংখ্যা, সেয়েহে, (x/y) – 6 হৈছে এক পৰিমেয় সংখ্যা, যি √2 অপৰিমেয় বুলি বিৰোধিতা কৰে।
সেয়েহে, আমি এই সিদ্ধান্তত উপনীত হ’ব পাৰোঁ যে 6 + √2 অপৰিমেয়।
বাস্তৱ সংখ্যা class 10
অনুশীলনী 1.4
1. প্ৰকৃততে দীঘলীয়া বিভাজন টো সম্পাদন নকৰাকৈ, নিম্নলিখিত যুক্তিসঙ্গত সংখ্যাবোৰৰ দশমিক সম্প্ৰসাৰণ সমাপ্ত হ’ব নে অসমাপ্ত দশমিক সম্প্ৰসাৰণ হ’ব:
(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2352) (vii) 129/(225775) (viii) 6/15 (ix) 35/50 (x) 77/210
সমাধানসমূহ:
টোকা: যদি হৰটোৰ উৎপাদক বোৰৰ গুণফল কেৱল 2 আৰু 5 থাকে বা 2m ×5n ৰূপত থাকে তেনেহ’লে ই দশমিক সম্প্ৰসাৰণ সমাপ্ত হ’ব।
যদি হৰটোৰ 2 আৰু 5-ৰ বাহিৰে আন মৌলিক উৎপাদক থাকে তেনেহ’লে ইয়াৰ দশমিক সম্প্ৰসাৰণ অসমাপ্ত হয়।
(i) 13/3125
হৰৰ উৎপাদক বোৰ, আমি পাওঁ,
3125 = 5 × 5 × 5 = 55
যিহেতু, হৰটোৰ উৎপাদক হিচাপে মাত্ৰ 5 আছে, 13/3125-ত দশমিক সম্প্ৰসাৰণ সমাপ্ত হৈছে।
(ii) 17/8
হৰৰ উৎপাদক বোৰ, আমি পাওঁ,
8 = 2×2×2 = 23
যিহেতু, হৰটোৰ উৎপাদক হিচাপে মাত্ৰ 3 আছে, 17/8-ত দশমিক সম্প্ৰসাৰণ সমাপ্ত হৈছে।
(iii) 64/455
হৰৰ উৎপাদক বোৰ, আমি পাওঁ,
455 = 5×7×13
যিহেতু, হৰটো 2m × 5n ৰূপত নহয়, সেয়েহে 64/455-ত দশমিক অসমাপ্ত ।
(iv) 15/ 1600
হৰৰ উৎপাদক বোৰ, আমি পাওঁ,
1600 = 26 52
যিহেতু, হৰটোৰ উৎপাদক হিচাপে মাত্ৰ 2m × 5n আছে, 15/ 1600-ত দশমিক সম্প্ৰসাৰণ সমাপ্ত হৈছে।


