| দুটা চলকযুক্ত ৰৈখিক সমীকৰণ | |
| বিষয় | গণিত |
| পাঠৰ নাম | দুটা চলকযুক্ত ৰৈখিক সমীকৰণ |
| অনুশীলন | 4.1, 4.2, 4.3 |
| শ্ৰেণী | নৱম |
| পাঠৰ নং | অধ্যায় ৪ |
| পাঠ্যক্ৰম | ছেবা |
দুটা চলকযুক্ত ৰৈখিক সমীকৰণ class 9
অনুশীলনী 4.1
১) এখন টোকা বহীৰ দাম এটা কলমৰ দামৰ দুগুণ। এই উক্তিটো প্রকাশ হােৱাকৈ দুটা চলকযুক্ত এটা ৰৈখিক সমীকৰণ গঠন কৰা। (ইয়াত এখন টোকাবহীৰ দাম x টকা আৰু এটা কলমৰ গম y টকা বুলি লােৱা)
সমাধান: ধৰা হল কলমৰ দাম y টকা আৰু টোকাবহীৰ দাম x টকা।
প্ৰশ্নমতে,
টোকাবহী এখনৰ দাম = কলমৰ দুগুণ = 2y।
∴2y = x
⇒ x – 2y = 0
এইটোৱে হৈছে উক্তিটো প্রকাশ হােৱা দুটা চলকযুক্ত ৰৈখিক সমীকৰণ।
2) তলৰ ৰৈখিক সমীকৰণবিলাক ax + by + c = 0 আর্হিত প্রকাশ প্রকাশ কৰা আৰু প্রতিটো ক্ষেত্রতে a b আৰু c মান উল্লেখ কৰা
(i) 2x + 3y = 9.35 (ii) x – y/5 – 10 = 0 (iii) -2x + 3y = 6 (iv) x = 3y
(v) 2x = -5y (vi) 3x + 2 = 0 (vii) y – 2 = 0 (viii) 5 = 2x
সমাধান:
(i) 2x + 3y = 9.35
⇒ 2x + 3y – 9.35 = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = 2x, b = 3 আৰু c = -9.35
(ii) x – y/5 – 10 = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = 1, b = -1/5 আৰু c = -10
(iii) -2x + 3y = 6
⇒ -2x + 3y – 6 = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = -2, b = 3 আৰু c = -6
iv) x = 3y
⇒ x – 3y = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = 1, b = -3 আৰু c = 0
(v) 2x = -5y
⇒ 2x + 5y = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = 2, b = 5 আৰু c = 0
(vi) 3x + 2 = 0
⇒ 3x + 0y + 2 = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = 3, b = 0 আৰু c = 2
(vii) y – 2 = 0
⇒ 0x + y – 2 = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = 0, b = 1 আৰু c = -2
(viii) 5 = 2x
⇒ -2x + 0y + 5 = 0
এই সমীকৰণটো ax + bx + c = 0 ৰ সৈতে তুলনা কৰিলে, আমি পাওঁ
a = -2, b = 0 আৰু c = 5
নৱম শ্ৰেণীৰ গণিত অধ্যায় 4
অনুশীলনী 4.2
1. তলত দিয়া সাম্ভাব্য উত্তৰকেইটা মাজৰ কোনটো সত্য আৰু কিয়?
y = 3x + 5 সমীকৰণটো
(i) এটা অদ্বিতীয় সমাধান আছে।
(ii) মাত্র দুটা সমাধান আছে।
(iii) অসীমসংখ্যক সমাধান আছে।
সমাধান: সমীকৰণটোৰ পৰা, y = 3x + 5 হৈছে দুটা চলকৰ এক ৰৈখিক সমীকৰণ। ইয়াৰ (iii) অসীমসংখ্যক সমাধান আছে।
2. তলতৰ প্ৰতিটো সমীকৰণৰ বাবে চাৰিটা সমাধান লিখক:
(i) 2x + y = 7 (ii) πx + y = 9 (iii) x = 4y
(i) 2x + y = 7
⇒ y = 7 – 2x
→ Put x = 0,
y = 7 – 2 × 0 ⇒ y = 7
(0, 7) হৈছে এটা সমাধান।
→ Now, put x = 1
y = 7 – 2 × 1 ⇒ y = 5
(1, 5) হৈছে এটা সমাধান।
→ Now, put x = 2
y = 7 – 2 × 2 ⇒ y = 3
(2, 3) হৈছে এটা সমাধান।
→ Now, put x = -1
y = 7 – 2 × -1 ⇒ y = 9
(-1, 9)হৈছে এটা সমাধান।
সমীকৰণটোৰ চাৰিটা সমাধান হৈছে (0, 7), (1, 5), (2, 3)আৰু (-1, 9).
(ii) πx + y = 9
⇒ y = 9 – πx
→ Put x = 0,
y = 9 – π×0 ⇒ y = 9
(0, 9)হৈছে এটা সমাধান।
→ Now, put x = 1
y = 9 – π×1 ⇒ y = 9-π
(1, 9-π) হৈছে এটা সমাধান।
→ Now, put x = 2
y = 9 – π×2 ⇒ y = 9-2π
(2, 9-2π) হৈছে এটা সমাধান।
→ Now, put x = -1
y = 9 – π× -1 ⇒ y = 9+π
(-1, 9+π)হৈছে এটা সমাধান।
সমীকৰণটোৰ চাৰিটা সমাধান হৈছে(0, 9), (1, 9-π), (2, 9-2π) আৰু (-1, 9+π).
(iii) x = 4y
→ Put x = 0,
0 = 4y ⇒ y = 0
(0, 0)হৈছে এটা সমাধান।
→ Now, put x = 1
1 = 4y ⇒ y = 1/4
(1, 1/4) হৈছে এটা সমাধান।
→ Now, put x = 4
4 = 4y ⇒ y = 1
(4, 1) হৈছে এটা সমাধান।
→ Now, put x = 8
8 = 4y ⇒ y = 2
(8, 2) হৈছে এটা সমাধান।
সমীকৰণটোৰ চাৰিটা সমাধান হৈছে (0, 0), (1, 1/4), (4, 1)আৰু (8, 2).
3. তলৰ কোনকেইটা ক্রমিক যুগল x – 2y = 4 ৰ সমাধান হয় আৰু কোনকেইটা নহয় পৰীক্ষা কৰা:
(i) (0, 2) (ii) (2, 0) (iii) (4, 0) (iv) (√2, 4√2) (v) (1, 1)
সমাধান:
(i) (0, 2)
x – 2y = 4 সমীকৰণটোত x=0 আৰু y= 2 বহুৱাই আমি পাওঁ
0 – 2×2 = 4
⇒ -4 ≠ 4
∴ (0, 2) প্ৰদত্ত সমীকৰণৰ সমাধান নহয়।
(ii) (2, 0)
x – 2y = 4 সমীকৰণটোত x=2 আৰু y= 0 বহুৱাই আমি পাওঁ
2 – 2×0 = 4
⇒ 2 ≠ 4
∴ (2, 0) প্ৰদত্ত সমীকৰণৰ সমাধান নহয়।
(iii) (4, 0)
x – 2y = 4 সমীকৰণটোত x=4 আৰু y= 0 বহুৱাই আমি পাওঁ
4 – 2×0 = 4
⇒ 4 = 4
∴ (4, 0) প্ৰদত্ত সমীকৰণৰ সমাধান হয়।
(iv) (√2, 4√2)
x – 2y = 4 সমীকৰণটোত x=√2 আৰু y=4√2 বহুৱাই আমি পাওঁ
√2 – 2×4√2 = 4
⇒ √2 – 8√2 = 4
⇒ √2(1 – 8) = 4
⇒ -7√2 ≠ 4
∴ (√2, 4√2) প্ৰদত্ত সমীকৰণৰ সমাধান নহয়।
(v) (1, 1)
x – 2y = 4 সমীকৰণটোত x=1 আৰু y=1 বহুৱাই আমি পাওঁ
1 – 2×1 = 4
⇒ -1 ≠ 4
∴ (1, 1) প্ৰদত্ত সমীকৰণৰ সমাধান নহয়।
4. যদি x = 2, y = 1 সমীকৰণ 2x+ 3y = k ৰ এটা সমাধান তেন্তে kৰ মান নির্ণয় কৰা।
সমাধান: প্ৰদত্ত সমীকৰণ = 2x + 3y = k
x = 2, y = 1 হৈছে প্ৰদত্ত সমীকৰণৰ সমাধান।
A/q,
সমীকৰণত x আৰু y মান বহুৱাই, আমি পাওঁ
2×2 + 3×1 = k
⇒ k = 4 + 3
⇒ k = 7
দুটা চলকযুক্ত ৰৈখিক সমীকৰণ 4.3
অনুশীলনী 4.3
1. তলত দিয়া দুটা চলকযুক্ত ৰৈখিক সমীৰণৰ প্ৰতিটোৰেই লেখ অংকন করা :
(i) x + y = 4 (ii) x – y = 2 (iii) y = 3x (iv) 3 = 2x + y
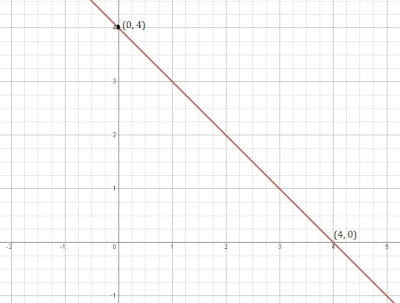
সমাধান: (i) x + y = 4
যদি, x = 0 তেন্তে y = 4 হৱ
আৰু x = 4 তেন্তে y = 0
| x | o | 4 |
| y | 4 | 0 |
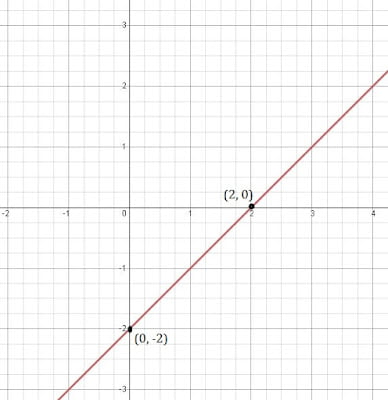
(ii) x – y = 2
যদি, x = 0 তেন্তে y = -2 হৱ
আৰু x = 2 তেন্তে y = 0
| x | o | 2 |
| y | -2 | 0 |
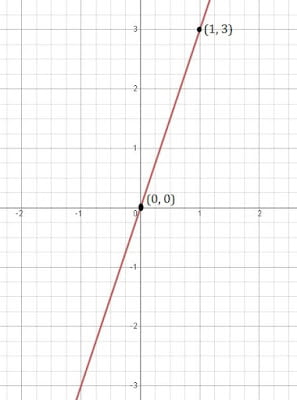
(iii) y = 3x
যদি, x = 0 তেন্তে y = 0 হৱ
আৰু x = 1 তেন্তে y = 3
| x | o | 1 |
| y | 0 | 3 |
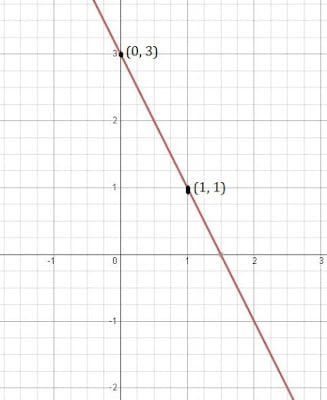
(iv) 3 = 2x + y
যদি, x = 0 তেন্তে y = 3 হৱ
আৰু x = 1 তেন্তে y = 1
| x | o | 1 |
| y | 3 | 1 |
2. (2,14) বিন্দুৰে যােৱা দুডাল ৰেখাৰ সমীকৰণ লিখা। এনেধৰণৰ আৰু কিমান ৰেখা আছে আৰু কিয়?
সমাধান: ইয়াত, x = 2 আৰু y =14।
এনেদৰে, x + y = 1
লগতে, y = 7 x ⇒ y – 7x = 0
∴ (2, 14) বিন্দুৰে পাৰ হৈ যোৱা দুডাল ৰেখাৰ সমীকৰণ হৈছে
x + y = 1 আৰু y – 7x = 0।
এনে ধৰণৰ অসীম ৰেখা থাকিব কিয়নো অসীম সংখ্যক ৰেখা এটা প্ৰদত্ত বিন্দুৰ মাজেৰে পাৰ হ’ব পাৰে।
3. যদি (3, 4) বিন্দুটো 3y = ax +7 সমীকৰণটোৰ লেখডালৰ ওপৰত থাকে তেনেহলে a ৰ মান উলিওৱা।
সমাধান: যদি (3, 4) বিন্দুটো 3y = ax +7 সমীকৰণটোৰ লেখডালৰ ওপৰত থাকে।
∴ 3y = ax +7 সমীকৰণত x = 3 আৰু y = 4, বহুৱাই আমি পাওঁ
3×4 = a×3 + 7
⇒ 12 = 3a + 7
⇒ 3a = 12 – 7
⇒ a = 5/3
4. এখন মহানগৰত টেক্সি ভাড়া এনেধৰণৰ :
প্রথম কিলােমিটাৰটোৰ বাবে ভাড়া ৪ টকা আৰু তাৰ পিছৰ দূৰত্ব ভাড়া হল প্রতি কিলােমিটাৰত 5 টকা। অতিক্রম কৰা দূৰত্ব x কিলােমিটাৰ আৰু মুঠা ভাড়া y টকা বুলি ধৰি এই তথ্যৰ ভিত্তিত এটা ৰৈখিক সমীকৰণ লিখা আৰু ইয়াৰ লেখ অংকন কৰা।
সমাধান: মুঠ ভাড়া = y
অতিক্ৰম কৰা মুঠ দূৰত্ব = x
প্ৰথম কিলোমিটাৰ পিছত পৰৱৰ্তী দূৰত্বৰ বাবে ভাড়া = 5 টকা
প্ৰথম কিলোমিটাৰৰ বাবে ভাড়া = 8 টকা
প্ৰশ্নমতে,
y = 8 + 5(x-1)
⇒ y = 8 + 5x – 5
⇒ y = 5x + 3
| x | 0 | -3/5 |
| y | 3 | 0 |
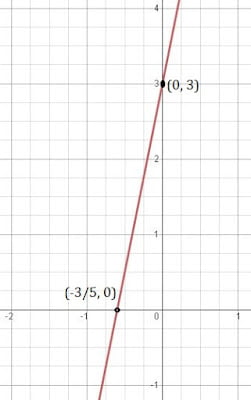
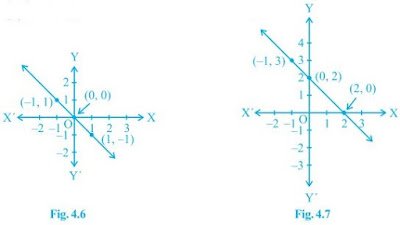
5. তলত দিয়া বিকল্পবিলাকৰ পৰা সমীকৰণ একোটা বাচনি কৰা যিটোৰ লেখ চিত্র 4.6 আৰু চিত্র 4.7 ত দিয়া হৈছে।
চিত্র 4.6 ৰ বাবে চিত্র 4.7 ৰ বাবে
(i) y = x (i) y = x + 2
(ii) x + y = 0 (ii) y = x – 2
(iii) y = 2x (iii) y = –x + 2
(iv) 2 + 3y = 7x (iv) x + 2y = 6
সমাধান:
চিত্র 4.6 ৰ বাবে, পইণ্টবোৰ হৈছে (0, 0), (-1, 1) আৰু (1, -1)।
∴ সমীকৰণ (ii) x + y = 0 শুদ্ধ কিয়নো ই বিন্দুবোৰৰ সকলো মূল সন্তুষ্ট কৰে।
চিত্র 4.7 ৰ বাবে, পইণ্টবোৰ হৈছে (-1, 3), (0, 2) আৰু (2, 0)।
∴ সমীকৰণ (iii) y = –x + 2 শুদ্ধ কিয়নো ই বিন্দুবোৰৰ সকলো মূল সন্তুষ্ট কৰে।
6. যদি এটা স্থিৰ (ধ্ৰুৱক) বল প্রয়ােগ কৰা ফলত কোনাে এটা বস্তুটোৱে অতিক্রম কৰা দূৰত্বৰ সমানুপাতিক হয় তেনেহ’লে এই তথ্য দুটা চলকযুক্ত ৰৈখিক সমীকৰণ এটাই প্ৰকাশ কৰা আৰু এই স্থিৰ বলক 5 একক ধৰি ইয়াৰ এটা লেখ অংকণ কৰা। তদুপৰি এই লেখৰ পৰা বস্তুটোৱে কৰা কার্য কিমান হব উলিওৱা যেতিয়া বস্তুটোৱে অতিক্রম কৰা দূৰত্ব হয়
(i) 2 একক
(ii) 0 একক
সমাধান: ধৰা হওক,
বস্তুটোৱে অতিক্রম কৰা দূৰত্ব x আৰু বস্তুটোৱে কৰা কার্য y।
y ∝ x (দিয়া আছে)
⇒ y = 5x (সমানুপাতিক সমান কৰিবলৈ, আমাক এটা ধ্ৰুৱকৰ প্ৰয়োজন। ইয়াত, ইয়াক 5 দিয়া হৈছে)
প্ৰশ্নমতে,
(i) যেতিয়া x = 2 একক তেতিয়া y = 10 একক
(ii) যেতিয়া x = 0 একক তেতিয়া y = 0 একক
| x | 2 | 0 |
| y | 10 | 0 |
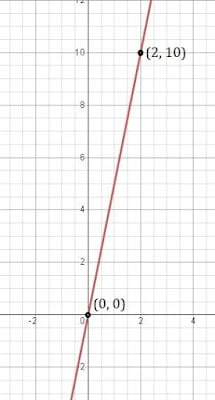
7. এখন স্কুলৰ নৱম শ্ৰেণীৰ দুজনী ছাত্রী যামিনী আৰু ফাতিমাই একেলগে ভূমিকম্প আক্রান্তসকলৰ বাবে প্রধানমন্ত্ৰীৰ সাহায্য পুঁজিলৈ 100 টকাৰ বৰঙণি আগবঢ়ালে। এই তথ্য সিদ্ধ কৰাকৈ এটা ৰৈখিক সমীকৰণ লিখ। (তেওঁলােকৰ বৰঙণিক x টকা আৰু y টকা বুলি ধৰিব পাৰা)। ইয়াৰ এটা লেখ অঁকা।
সমাধান: ধৰা হওক,
যামিনীৰ বৰঙণিক x টকা আৰু ফাতিমাৰ বৰঙণিক y টকা বুলি ধৰিব পাৰা
প্ৰশ্নমতে,
x + y = 100
যেতিয়া x = 0 তেতিয়া y = 100
যেতিয়া x = 50 তেতিয়া y = 50
যেতিয়া x = 100 তেতিয়া y = 0
| x | 0 | 50 | 100 |
| y | 100 | 50 | 0 |
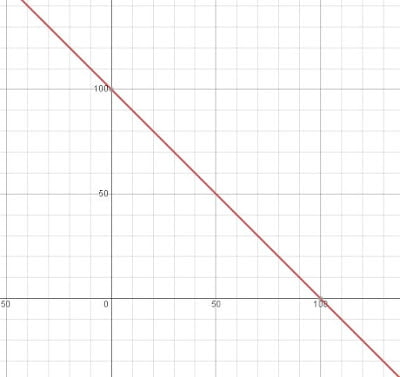
8. আমেৰিকা যুক্তৰাষ্ট্র, কানাডা আদিৰ দৰে দেশত উষ্ণতাক ফাৰেনহেইট এককৰে জোখা হয়, কিন্তু ভাৰতৰ দৰে দেশক ইয়াক চেলচিয়াছ এককৰে জোখে। তলত এটা ৰৈখিক সমীকৰণ দিয়া হল যিটো সহায়ত ফাৰেনহেইটক চেলচিয়াছ লৈ পৰিৱৰ্তন কৰা হয়।

