SEBA Class 10 Maths Solution chapter 3
[showhide type=”post” more_text=”Show More…” less_text=”show less…”] SEBA Class 10 Maths Solution chapter 3 in Assamese – দুটা চলকত ৰৈখিক সমীকৰণৰ যোৰ দশম শ্ৰেণীৰ অংক সমাধান help the students in understanding how the problems under this concept are solved. Maths is one subject that requires a lot of practice. [/showhide]দুটা চলকত ৰৈখিক সমীকৰণৰ যোৰ
অনুশীলনী 3.1
1) 7 বছৰ আগতে আফটাৱে তেওঁ ছোৱালীৰ বয়সৰ.7 গুণ আছিল। এতিয়াৰ পৰা তিনিবছৰ,পিছত আফটাব জীয়েকৰ বয়সৰ তিনিগুণ হ’ব। উক্ত সমীকৰণক বীজগণিতীয় ৰূপত আৰু লেখৰ সহায়ত উপস্থাপন কৰা।
সমাধান: ধৰাহ’ল আফটাবৰ বৰ্ত্তমান বয়স x আৰু ছোৱালীৰ বৰ্ত্তমান বয়স y বছৰ।
7 বছৰ আগতে তে তেওঁলোকৰ বয়স আছিল ক্ৰমে (x-7) বছৰ আৰু (y-7) বছৰ।
প্ৰশ্ন অনুসৰি,
x−7 = 7(y−7)
⇒x−7 = 7y−49
⇒x−7y = −42 —(i)
লগতে, এতিয়াৰ পৰা তিনি বছৰৰ পিছত
আফতাবৰ বয়স হ’ব =x+3
তেওঁৰ জীয়েকৰ বয়স হ’ব = y+3
দিয়া পৰিস্থিতি অনুসৰি,
x+3 = 3(y+3)
⇒x+3 = 3y+9
⇒x−3y = 6 —(ii)
সমীকৰণ (ii)ৰ পৰা সমীকৰণ (i) বিয়োগ কৰি পাওঁ
(x−3y)−(x−7y) = 6−(−42)
⇒−3y+7y = 6+42
⇒4y = 48
⇒y = 12
উক্ত সমীকৰণক বীজগণিতীয় ৰূপত
x−7y = −42
⇒ x−7y = −42
⇒x = −42+7y
সমাধান তালিকা হৈছে
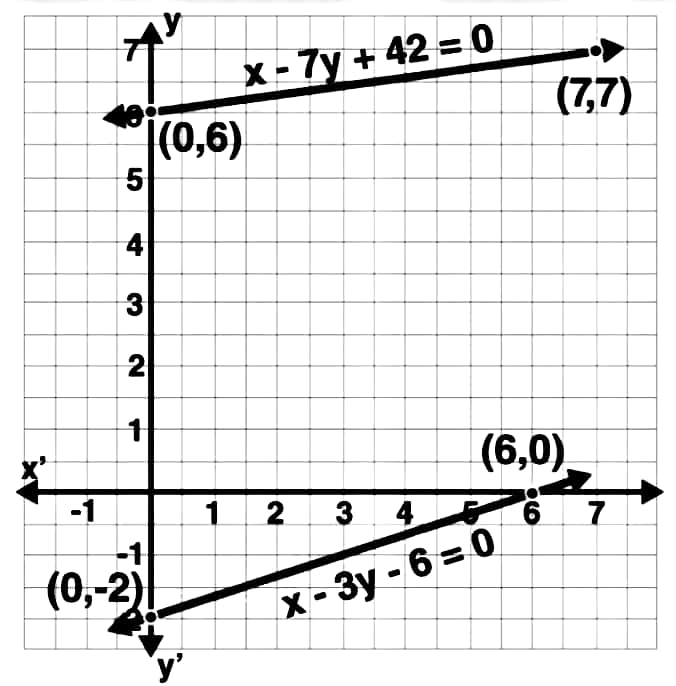
| x | -7 | 0 | 7 |
| y | 5 | 6 | 7 |
আকৌ দ্বিতীয় সমীকৰণৰ পৰা
x−3y = 6
x = 6+3y
সমাধান তালিকা হৈছে
| x | 6 | 4 | 0 |
| y | 0 | -1 | -2 |
লেখৰ সহায়ত উপস্থাপন
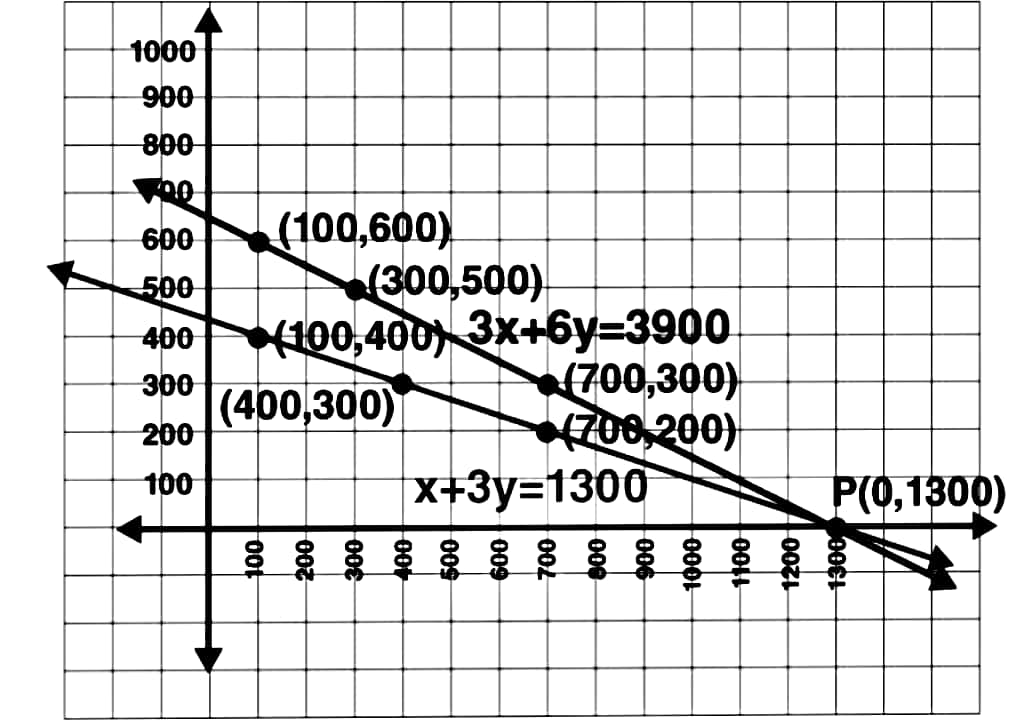
2. এজন ক্ৰিকেট প্ৰশিক্ষকে এখন বেট আৰু 6টা বল 3900 টকাত কিনিলে পিছত তাই অন্য এখন বেট আৰু একে ধৰণৰ 2টা বল কিনিলে ইয়াৰ মূল্য 1300টকা। উক্ত কথাখিনি বীজগণিতীয় ৰাশিত প্ৰকাশ কৰা আৰু লেখৰ সহায়ত মান নিৰ্ণয় কৰা।
সমাধানঃ ধৰাহ’ল এখন বেট আৰু এটা বলৰ দাম ক্ৰমে x আৰু y
১ম চৰ্ত্ত মতে,
তিনিখন বেটৰ দাম = 3x
6টা বলৰ = 6y
3x+6y = 3900
⇒ x+2y = 1300
x=1300-2y
সমাধান তালিকা হৈছে
| x | 1300 | 700 | 300 |
| y | 0 | 300 | 500 |
2য় চৰ্ত্ত মতে,
এখন বেটৰ দাম = x
তিনিটা বলৰ = 3y
x+3y = 1300
⇒ x = 1300-3y
সমাধান তালিকা হৈছে
| x | 400 | 100 | 1300 |
| y | 300 | 400 | 0 |
লেখত উপস্থাপন—
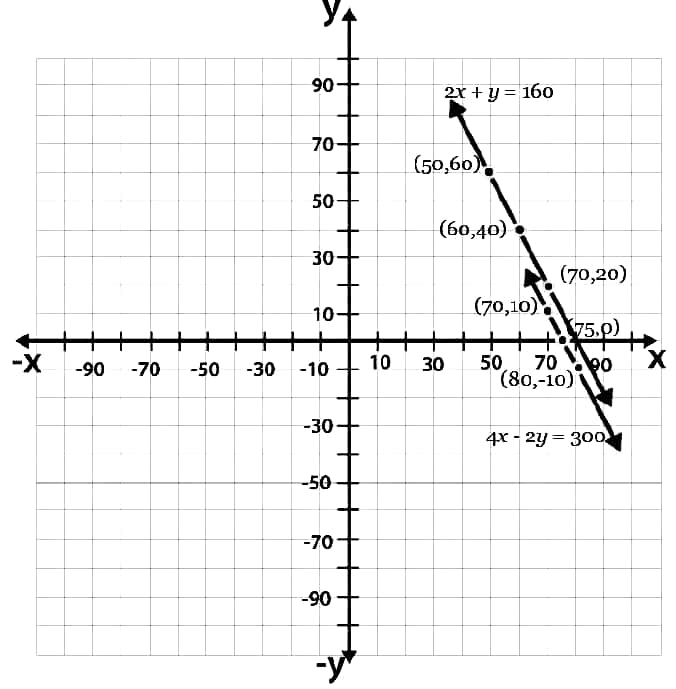
2. 2kg আপেল আৰু 1kg আঙুৰৰ দাম 1600 টকা ৷ এমাহ পিছত 4kg আপেল আৰু 2kg আঙুৰৰ দাম 300 টকা৷ উক্ত কথাখিনি বীজগণিতীয় ৰাশিত প্ৰকাশ কৰা লগতে লেখত উপস্থাপন কৰা ৷
সমাধান : ধৰাহ’ল,
1kg আপেলৰ দাম x টকা আৰু
1kg আঙুৰৰ দাম y টকা ৷
বীজগণিতীয় উপস্থাপন
১ম চৰ্ত্ত মতে,
2x+y = 160 —(i)
⇒ y = 160−2x
সমাধান তালিকা হৈছে
| x | 50 | 60 | 70 |
| y | 60 | 40 | 20 |
2য় চৰ্ত্ত মতে,
4x+2y = 300
⇒ y = (300-4x)/2
সমাধান তালিকা হৈছে
| x | 70 | 80 | 75 |
| y | 10 | -10 | 0 |
লেখত উপস্থাপন