| বিষয় | নৱম শ্ৰেণীৰ গণিত অধ্যায় 5 সমাধান |
| অনুশীলনী | 5.1 And 5.2 |
| অধ্যায়ৰ নাম | ইউক্লিডৰ জ্যামিতি |
নৱম শ্ৰেণী গণিত অধ্যায় 5
অনুশীলনী 5.1
1. তলৰ কোনবােৰ উক্তি সত্য আৰু কোনবোৰ অসত্য। তােমাৰ উত্তৰৰ সপক্ষে কাৰণ দেখুওৱা।
(i) এটা বিন্দু মাজেৰে মাথোঁ এডাল ৰেখাহে পাব পাৰি।
(ii) দুটা বিন্দু মাজেৰে অসীম সংখাক ৰেখা পাব পাৰি।
(iii) এডাল সীমিত ৰেখাখণ্ডক অসীমাভাবে দুই মুৰে বৃদ্ধি কৰিব পাৰি।
(iv) যদি দুটা বৃত্ত সমান, তেন্তে সিহতৰ ব্যাসার্ধও সমান।
(v) চিত্র 5.9 ত যদি AB = PQ আৰু PQ = XY, তেন্তে AB = XY)
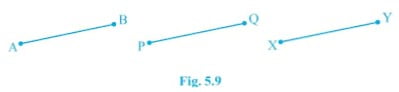
উত্তৰ:
(i) অসত্য। এটা বিন্দুৰ মাজেৰে অসীম ৰেখা আঁকিব পাৰি।
(ii) অসত্য। দুটা বিন্দু মাজেৰে কেৱল এডাল ৰেখা আঁকিব পাৰি।
(iii) সত্য। এডাল সীমিত ৰেখাখণ্ডক অসীমাভাবে দুই মুৰে বৃদ্ধি কৰিব পাৰি।
জ্যামিতিত, ৰেখা এডাল দুয়ো দিশত বৃদ্ধি কৰিব পাৰি। ৰেখা এডালৰ অৰ্থ হৈছে অসীম দীঘল দৈৰ্ঘ্য।
(iv) সত্য। যদি দুটা বৃত্ত সমান হয়, তেন্তে সিহতৰ ব্যাসার্ধও সমান।
(v) সত্য। ইউক্লিডৰ প্ৰথম স্বতঃসিদ্ধ মতে।
class 9 maths 5.1 assamese
2. তলৰ প্ৰতিটো পদৰ সংজ্ঞা দিয়া। তাত কিবা আন পদ আছে নেকি যাৰ প্রথমে সংজ্ঞা দিয়া প্ৰয়োজন? সেইবোৰ কি আৰু তুমি কেনেকৈ সেইবোৰ সংজ্ঞা দিবা।
(i) সমান্তৰাল ৰেখা (ii) লম্ব ৰেখা (iii) ৰেখা খণ্ড (iv) এটা বৃত্তৰ ব্যাসার্ধ (v) বৰ্গ
উত্তৰ: হয়, আন পদৰ প্ৰথমে প্রথমে সংজ্ঞা দিয়া প্ৰয়োজন যিবোৰ হৈছে:
সমতল: এখন সমতল পৃষ্ঠ য’ত জ্যামিতিক চিত্ৰ অংকন কৰা হয়।
বিন্দু: এটা বিন্দু হৈছে সমতল পৃষ্ঠত অঁকা বিন্দু আৰু মাত্ৰাহীন।
ৰেখা: এটা ৰেখা হৈছে বিন্দুৰ সংগ্ৰহ যি দুয়োদিশত প্ৰসাৰিত হ’ব পাৰে।
(i) সমান্তৰাল ৰেখা: যেতিয়া সমতলত দুই বা ততোধিক ৰেখাক দুয়োফালে বঢ়াই দিলে এডালে আনডালক কেতিয়াও ছেদ নকৰে আৰু সিহঁতৰ মাজত লম্ব দূৰত্ব সদায় স্থিৰ থাকে তেতিয়া সেইবোৰ ৰেখাক সমান্তৰাল ৰেখা বুলি কোৱা হয়।
(ii) লম্ব ৰেখা: যেতিয়া দুডাল ৰেখাই এডালে আনডালক সমতলত সমকোণত ছেদ কৰে তেতিয়া সেইবোৰ ৰেখাক লম্ব বুলি কোৱা হয়।
(iii) ৰেখা খণ্ড: এডাল ৰেখা খণ্ড হৈছে দুটা অন্তিম বিন্দুৰ সৈতে এডাল ৰেখাৰ অংশ আৰু ইয়াক আৰু সম্প্ৰসাৰিত কৰিব নোৱাৰি।
(iv) বৃত্তৰ ব্যাসাৰ্ধ: কেন্দ্ৰ আৰু বৃত্তৰ পৰিধিৰ মাজৰ স্থিৰ দূৰত্বক বৃত্তৰ ব্যাসাৰ্ধ বুলি কোৱা হয়।
(vi) বৰ্গ: বৰ্গ হৈছে এক চতুৰ্ভুজ য’ত চাৰিওটা বাহু সমান আৰু প্ৰতিটো আভ্যন্তৰীণ কোণ সমকোণ।
ইউক্লিডৰ জ্যামিতি Class IX
3. তলত দিয়া স্বীকাৰ্য দুটা বিবেচনা কৰা:
(i) প্রদত্ত দুটা নিৰ্দিষ্ট বিন্দু A আৰু B ৰ বাবে তৃতীয় এটা বিন্দু C পােৱা যায় যি A আৰু B মাজত অবস্থিত।
(ii) একে ৰেখাত নাথাকিবলৈ হ’লে অতি কমেও তিনিটা বিন্দু থাকে।
এই স্বীকার্য দুটাত কিবা সংজ্ঞাহীন পদ আছেনে? এই দুটা স্বীকার্য সংগত নে? সিইতে ইউক্লিডন স্বীকাৰ্য মানি লয়নে? ব্যাখ্যা কৰা
উত্তৰ: এই স্বীকার্য দুটাৰ সংজ্ঞাহীন পদ আছে। সেইবোৰ হল-
বহুতো বিন্দু এখন সমতলত থাকে। কিন্তু ইয়াত C বিন্দু স্থিতিৰ বিষয়ে দিয়া হোৱা নাই যে ই AB ৰেখাখণ্ডত আছে নে নাই। লগতে, সমতলৰ বিষয়ে কোনো তথ্য নাই যে বিন্দুবোৰ একেখন সমতলত আছে নে নাই। হয়, যেতিয়া আমি এই দুটা পৰিস্থিতিৰ সৈতে মোকাবিলা কৰোঁ তেতিয়া এই স্বীকার্য সংগত হয় | সিইতে ইউক্লিডন স্বীকাৰ্য মানি নলয়
4. যদি এটা বিন্দু C. দুটা বিন্দু A আৰু B ৰ মাজত থাকে যাতে AC = BC. তেন্তে প্রমাণ কৰা যে AC= 1/2AB। চিত্ৰ সহ ব্যাখ্যা কৰা।
সমাধান:
![]()
চিত্রত, C বিন্দুটো A আৰু B বিন্দুৰ মাজত আছে যাতে AC = BC
∴ AC + AC = BC + AC (দুয়ােফালে সমান অংশ যােগ কৰি)
⇒ 2AC = AB
⇒ AC = ½AB
5. 4নং প্রশ্নত C বিন্দুক AB ৰেখাখণ্ডৰ মধ্যবিন্দু বোলে। প্রমাণ কৰা যে , যিকোনো ৰেখা খণ্ডৰ এটা আৰু এটাহে মধ্য বিন্দু থাকে।
6. চিত্র 5.0 ত, যদি AC = BD, তেন্তে প্রমাণ কৰা যে AB = CD
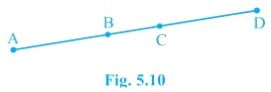
সমাধানঃ চিত্ৰৰ পৰা, AC = BD
⇒ AB + BC = BC+ CD
⇒ AB + BC – BC – BC + CD – BC
⇒ AB = CD
class 9 maths 5.2 assamese
অনুশীলনী 5.2
প্রশ্ন : ইউক্লিডৰ পঞ্চম স্বীকাৰ্যটো সহজে বােধগম্য হােৱাকৈ লিখা।
উত্তৰ : AB আৰু CD ৰেখাদুডালক PQ ছেদকে R আৰু S বিন্দুত কাটিছে যাতে
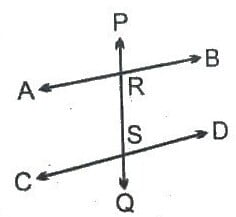
∠ARS + ∠CSR ∠ 180°
AB আৰু CD ক A আৰু C অভিমুখে বঢ়াই দিলে এটা বিন্দুত ছেদ কৰিব।
২. ইউক্লিডৰ পঞ্চম স্বীকাৰ্যটো সমান্তৰাল ৰেখাৰ অৱস্থিতি সূচায়নে? ব্যাখ্যা কৰা।
উত্তৰ : হয়, ইউক্লিডৰ পঞ্চম স্বীকাৰ্যটো সমান্তৰাল ৰেখাৰ অৱস্থিতি সূচায়।
যদি ৰেখা দুডালৰ অন্তকোন দুটাৰ যোগফল দুই সমকোনৰ সমান হয় তেন্তে ৰেখা দুডালে পৰস্পৰ লগ নালাগে। গতিকে ৰেখা দুডাল সমান্তৰাল হব।
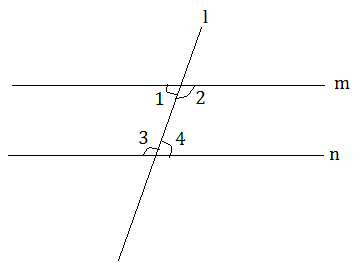
যদি m আৰু n সমান্তৰাল হব
∠1 + ∠3 = 180°
বা ∠3 + ∠4 = 180°
_________________
ইউক্লিডৰ জ্যামিতি – নৱম শ্ৰেণী গণিত অধ্যায় 5 সমাধান Class 9 Maths Chapter 5 solution in Assamese Medium

