বহুপদ দশম শ্ৰেণীৰ গণিত অধ্যায় 2 [সমাধান]

বহুপদ দশম শ্ৰেণী

বহুপদ
বিষয় (Subject)	গণিত (Mathematics)
কিতাপখনৰ নাম	সাধাৰণ গণিত
পাঠৰ নাম	বহুপদ
শ্ৰেণী (Class)	দশম শ্ৰেণীৰ গণিত (X)
অধ্যায় (Chapter)	অধ্যায় 2
অনুশীলনী	2.1, 2.2, 2.3
পাঠ্যক্ৰম (Syllabus)	ছেবা (SEBA)

দশম শ্ৰেণীৰ গণিত বহুপদ

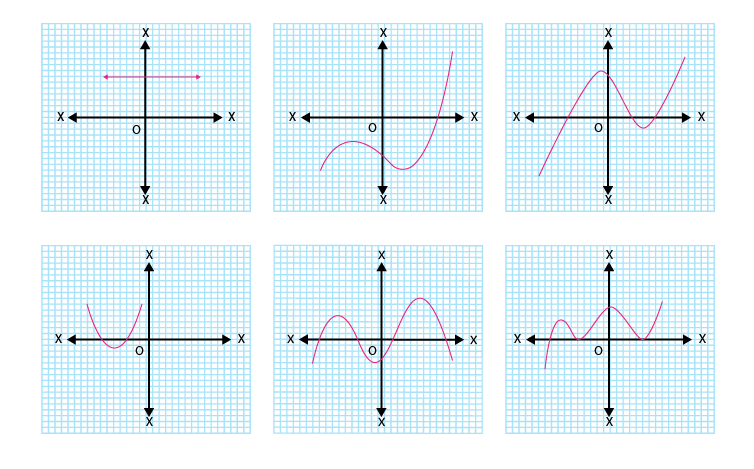
1. কিছুমান বহুপদ p(x)অৰ ক্ষেত্ৰত y=p(x) ৰ লেখবোৰ তলৰ চিত্ৰত দিয়া আছে। প্ৰতিটো ক্ষেত্ৰত p(x)ৰ শূণ্য সংখ্যা উলিওৱা।

সমাধানসমূহ:

শূন্য বিচাৰিবলৈ গ্ৰাফিকেল পদ্ধতি:-

যিকোনো বহুপদ সমীকৰণত মুঠ শূন্যৰ সংখ্যা = বক্ৰই x-অক্ষক ছেদ কৰাৰ মুঠ সংখ্যা।

(i) প্ৰদত্ত লেখত, p(x)ৰ শূন্যৰ সংখ্যা 0 হয় কিয়নো গ্ৰাফটো x-অক্ষৰ সমান্তৰাল হয় আৰু ইয়াক কোনো সময়তে কাটি নিদিয়ে।

(ii) প্ৰদত্ত লেখত, p(x)ৰ শূন্যৰ সংখ্যা হৈছে 1 কিয়নো গ্ৰাফে কেৱল এটা বিন্দুত x-অক্ষক ছেদ কৰে।

(iii) প্ৰদত্ত লেখত, p(x)ৰ শূন্যৰ সংখ্যা 3 হয় কিয়নো গ্ৰাফে যিকোনো তিনিটা বিন্দুত x-অক্ষক ছেদ কৰে।

(iv) প্ৰদত্ত লেখত, p(x)ৰ শূন্যৰ সংখ্যা 2 হয় কিয়নো গ্ৰাফে x-অক্ষক দুটা বিন্দুত ছেদ কৰে।

(v) প্ৰদত্ত লেখত, p(x)ৰ শূন্যৰ সংখ্যা 4 হয় কিয়নো গ্ৰাফে x-অক্ষক চাৰিটা বিন্দুত ছেদ কৰে।

(vi) প্ৰদত্ত লেখত, p(x)ৰ শূন্যৰ সংখ্যা 3 হয় কিয়নো গ্ৰাফে x-অক্ষক তিনিটা বিন্দুত ছেদ কৰে।

Also Read: Class 10 Maths Chapter 1 Assamese Medium

বহুপদ class 10

Exercise 2.2

1. তলৰ দ্বিঘাত বহুপদবোৰৰ শূণ্য উলিওৱা আৰু এই সুনীবোৰ আৰু সহগবোৰৰ মাজত সম্পৰ্ক সত্যাপন কৰা।

সমাধানসমূহ:

(i) x²–2x –8

⇒x²– 4x+2x–8

= x(x–4)+2(x–4)

= (x-4)(x+2)

সেয়েহে, বহুপদ সমীকৰণৰ শূন্যবোৰ হৈছে (4, -2)

শূন্যৰ যোগফল= 4–2 = 2 =-(-2)/1 (x ৰ সহগ/x² ৰ সহগ)

শূণ্যৰ পুৰণফল = 4×(-2) = -8 =-(8)/1 ধ্ৰুৱক/x² ৰ সহগ

(ii) 4s²–4s+1

⇒4s²–2s–2s+1

= 2s(2s–1)–1(2s-1)

= (2s–1)(2s–1)

সেয়েহে, বহুপদ সমীকৰণৰ শূন্যবোৰ হৈছে  (1/2, 1/2)

শূন্যৰ যোগফল= (½)+(1/2) = 1 = -4/4 = (x ৰ সহগ/x² ৰ সহগ)

শূণ্যৰ পুৰণফল= (1/2)×(1/2) = 1/4 = ধ্ৰুৱক/x² ৰ সহগ

(iii) 6x²–3–7x

⇒6x²–7x–3 = 6x² – 9x + 2x – 3

= 3x(2x – 3) +1(2x – 3)

= (3x+1)(2x-3)

সেয়েহে, বহুপদ সমীকৰণৰ শূন্যবোৰ হৈছে (-1/3, 3/2)

শূন্যৰ যোগফল= -(1/3)+(3/2) = (7/6) = (x ৰ সহগ/x² ৰ সহগ)

শূণ্যৰ পুৰণফল = -(1/3)×(3/2) = -(3/6) = ধ্ৰুৱক/x² ৰ সহগ

(iv) 4u²+8u

⇒ 4u(u+2)

বহুপদ সমীকৰণৰ শূন্যবোৰ হৈছে (0, -2).

শূন্যৰ যোগফল = 0+(-2) = -2 = -(8/4) =  (x ৰ সহগ/x² ৰ সহগ)

শূণ্যৰ পুৰণফল = 0×-2 = 0 = 0/4 = ধ্ৰুৱক/x² ৰ সহগ

(v) t²–15

⇒ t² = 15 or t = ±√15

বহুপদ সমীকৰণৰ শূন্যবোৰ হৈছে  (√15, -√15)

শূন্যৰ যোগফল =√15+(-√15) = 0= -(0/1)=  (x ৰ সহগ/x² ৰ সহগ)

শূণ্যৰ পুৰণফল = √15×(-√15) = -15 = -15/1 =  ধ্ৰুৱক/x² ৰ সহগ

(vi) 3x²–x–4

⇒ 3x²–4x+3x–4

= x(3x-4)+1(3x-4)

= (3x – 4)(x + 1)

বহুপদ সমীকৰণৰ শূন্যবোৰ হৈছে  (4/3, -1)

শূন্যৰ যোগফল = (4/3)+(-1) = (1/3)= -(-1/3) =  (x ৰ সহগ/x² ৰ সহগ)

শূণ্যৰ পুৰণফল=(4/3)×(-1) = (-4/3) = ধ্ৰুৱক/x² ৰ সহগ

বহুপদ দশম শ্ৰেণী

2. তলৰ যোৰকেইটা সংখ্যা দুটাক ক্ৰমে শূন্যবোৰৰ সমষ্টি আৰু গুণফল হিচাপে ধৰি প্ৰত্যেকৰ ক্ষেত্ৰত একোটা দ্বিঘাত বহুপদ নিৰ্ণয় কৰা।

(i) 1/4 , -1

সমাধান:

আমি জানো,

শূন্যৰ সমষ্টি = α+β = 1/4

শূন্যৰ গুণফল = α β = -1

∴ যদি α আৰু β যিকোনো দ্বিঘাত বহুপদৰ শূন্য হয়, তেন্তে দ্বিঘাত বহুপদ সমীকৰণটো পোনপটীয়াকৈ এনেদৰে লিখিব পাৰি:-

x²–(α+β)x +αβ = 0

x²–(1/4)x +(-1) = 0

4x²–x-4 = 0

দ্বিঘাত বহুপদ সমীকৰণটো 4x²–x-4 = 0

(ii)√2, 1/3

আমি জানো,

শূন্যৰ সমষ্টি = α + β =√2

শূন্যৰ গুণফল = α β = 1/3

∴ যদি α আৰু β যিকোনো দ্বিঘাত বহুপদৰ শূন্য হয়, তেন্তে দ্বিঘাত বহুপদ সমীকৰণটো পোনপটীয়াকৈ এনেদৰে লিখিব পাৰি:-

x²–(α+β)x +αβ = 0

x² –(√2)x + (1/3) = 0

3x²-3√2x+1 = 0

দ্বিঘাত বহুপদ সমীকৰণটো 3x²-3√2x+1 = 0

(iii) 0, √5

আমি জানো,

শূন্যৰ সমষ্টি = α+β = 0

শূন্যৰ গুণফল = α β = √5

∴ যদি α আৰু β যিকোনো দ্বিঘাত বহুপদৰ শূন্য হয়, তেন্তে দ্বিঘাত বহুপদ সমীকৰণটো পোনপটীয়াকৈ এনেদৰে লিখিব পাৰি:-

x²–(α+β)x +αβ = 0

x²–(0)x +√5= 0

দ্বিঘাত বহুপদ সমীকৰণটো x²–(0)x +√5= 0

(iv) 1, 1

আমি জানো,

শূন্যৰ সমষ্টি =  α+β = 1

শূন্যৰ গুণফল = α β = 1

∴ যদি α আৰু β যিকোনো দ্বিঘাত বহুপদৰ শূন্য হয়, তেন্তে দ্বিঘাত বহুপদ সমীকৰণটো পোনপটীয়াকৈ এনেদৰে লিখিব পাৰি:-

x²–(α+β)x +αβ = 0

x²–x+1 = 0

দ্বিঘাত বহুপদ সমীকৰণটো x²–x+1 = 0

(v) -1/4, 1/4

আমি জানো,

শূন্যৰ সমষ্টি = α+β = -1/4

শূন্যৰ গুণফল = α β = 1/4

∴ যদি α আৰু β যিকোনো দ্বিঘাত বহুপদৰ শূন্য হয়, তেন্তে দ্বিঘাত বহুপদ সমীকৰণটো পোনপটীয়াকৈ এনেদৰে লিখিব পাৰি:-

x²–(α+β)x +αβ = 0

x²–(-1/4)x +(1/4) = 0

4x²+x+1 = 0

দ্বিঘাত বহুপদ সমীকৰণটো 4x²+x+1 = 0

(vi) 4, 1

আমি জানো,

শূন্যৰ সমষ্টি = α+β = 4

শূন্যৰ গুণফল =  αβ = 1

∴ যদি α আৰু β যিকোনো দ্বিঘাত বহুপদৰ শূন্য হয়, তেন্তে দ্বিঘাত বহুপদ সমীকৰণটো পোনপটীয়াকৈ এনেদৰে লিখিব পাৰি:-

x²–(α+β)x+αβ = 0

x²–4x+1 = 0

দ্বিঘাত বহুপদ সমীকৰণটো x²–4x+1 = 0

দশম শ্ৰেণীৰ গণিত বহুপদ

Exercise 2.3

1. P(x) বহুপদটোক g(x) বহুপদটোয়ে হৰণ কৰা আৰু প্ৰতিটোৰে ক্ষেত্ৰত ভাগফল আৰু ভাগশেষ নিৰ্ণয় কৰা:

(i) p(x) = x³-3x²+5x–3 , g(x) = x²–2

সমাধান:

দিয়া আছে,

ভাজক= p(x) = x³-3x²+5x–3

ভাজ্য= g(x) = x²– 2

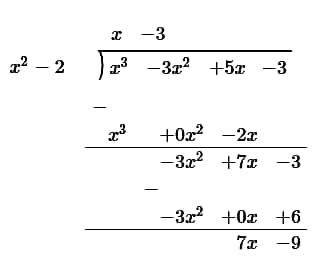
ভাগফল =x–3

ভাগশেষ = 7x–9

(ii) p(x) = x⁴-3x²+4x+5 , g(x) = x²+1-x

সমাধান:

দিয়া আছে,

ভাজক= p(x) = x⁴ – 3x² + 4x +5

ভাজ্য=  g(x) = x² +1-x

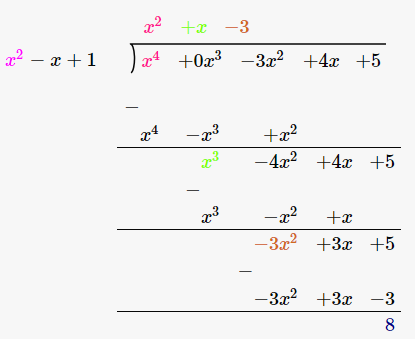
ভাগফল =x² + x–3

ভাগশেষ = 8

(iii) p(x) =x⁴–5x+6, g(x) = 2–x²

সমাধান:

দিয়া আছে,

ভাজক= p(x) =x⁴ – 5x + 6 = x⁴ +0x²–5x+6

ভাজ্য=  g(x) = 2–x² = –x²+2

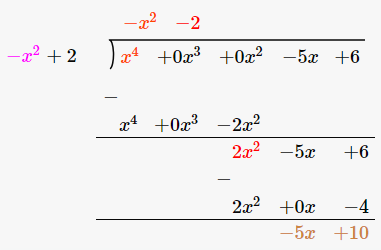
ভাগফল =-x²-2

ভাগশেষ = -5x + 10

দশম শ্ৰেণীৰ গণিত বহুপদ

2. দ্বিতীয় বহুপদটোক প্ৰথম বহুপদেৰে হৰণ কৰি প্ৰথম বহুপদটো দ্বিতীয় বহুপটোৰ এটা উৎপাদক হয়নে নহয় পৰীক্ষা কৰা।

(i) t²-3, 2t⁴ +3t³-2t²-9t-12

সমাধান:

দিয়া আছে,

প্ৰথম বহুপদ=t²-3

দ্বিতীয় বহুপদ= 2t⁴ +3t³-2t² -9t-12

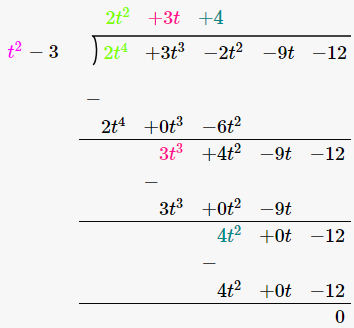
যিহেতু আমি ইয়াত ভাগশেষ শূণ্য পাইছোঁ গতিকে প্ৰথম বহুপদটো দ্বিতীয় বহুপদটোৰ এটা উৎপাদক হয়।

(ii) x²+3x+1 , 3x⁴+5x³-7x²+2x+2

সমাধান:

দিয়া আছে,

প্ৰথম বহুপদ= x²+3x+1

দ্বিতীয় বহুপদ= 3x⁴+5x³-7x²+2x+2

যিহেতু আমি ইয়াত ভাগশেষ শূণ্য পাইছোঁ গতিকে প্ৰথম বহুপদটো দ্বিতীয় বহুপদটোৰ এটা উৎপাদক হয়।

(iii) x³-3x+1, x⁵-4x³+x²+3x+1

সমাধান:

দিয়া আছে,

প্ৰথম বহুপদ= x³-3x+1

দ্বিতীয় বহুপদ= x⁵-4x³+x²+3x+1

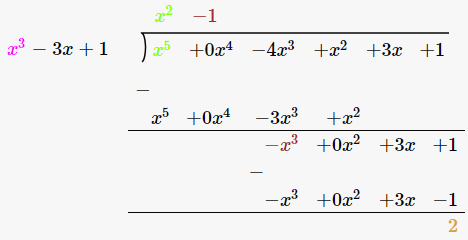
যিহেতু  ইয়াত ভাগশেষ শূণ্য নহয় গতিকে প্ৰথম বহুপদটো দ্বিতীয় বহুপদটোৰ এটা উৎপাদক নহয়।

দশম শ্ৰেণীৰ গণিত বহুপদ

3. যদি দুটা শূন্য √(5/3) আৰু – √(5/3), তেন্তে  3x⁴+6x³-2x²-10x-5 ৰ বাকী আটাইবোৰ শূণ্য উলিওৱা